Сайт Александра Зеленина

Александр Зеленин.

Введение в метод FDTD.

Аббревиатура FDTD расшифровывается как "finite-difference time-domain", а в русскоязычной литературе иногда выглядит как КРВО - "конечные разности во временной области", что является переводом с английского. В принципе этот метод - понятие чисто математическое и обозначает один из многочисленных методов решения дифференциальных уравнений, но среди тех, кто занимается решением задач электротехники, аббревиатура FDTD в настоящее время является синонимом решения вихревых дифференциальных уравнений Максвелла.

В 1966 г. Йе (Yee) разработал технику, реализующую явную конечно - разностную схему второго порядка для решения вихревых уравнений Максвелла в пространстве и времени.

Исходными являются уравнения Максвелла в дифференциальной форме:

а также

Здесь E - вектор напряженности электрического поля (В/м), Н - вектор напряженности магнитного поля (А/м), ε, μ - относительные диэлектрическая и магнитная проницаемости (без размерности), ε_o - диэлектрическая постоянная (Ф/м), μ_o - магнитная постоянная (Гн/м), B - вектор магнитной индукции (Тл), D - вектор электрического смещения (Кл/м²), J - вектор плотности тока (А/м²), σ - электрическая проводимость (См/м), и t - время в секундах.

ε_o = 10⁷/(4pc²), где с - скорость света в вакууме (2,997925010 x 10⁸ м/с).

μ_o = 4p/10⁷.

Оба уравнения (1) содержат пространственные и временные производные.

Для решения уравнения (1) следует выразить в декартовых координатах векторы Е и Н:

где E_x, E_y, E_z, H_x, H_y, H_z - проекции векторов на координатные оси, а X, Y, Z - единичные векторы.

Остальные величины в (1) - D, B, J - выразим через E и H. Величины E и H для нас будут основными.

Примечание: существуют и другие подходы, когда в уравнениях (1) вначале оставляют D и/или B, но в конце концов всё равно выражаются вектора Е и Н . Также следует указать, что уравнения (1) записаны не полностью. Например, в них не учитываются сторонние токи.

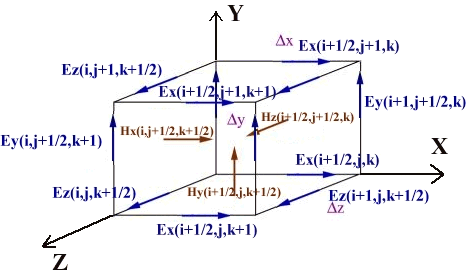
Yee (1966) предложил пространственную сетку для конечно-разностной аппроксимации, в которую поместил вектора E_x, E_y, E_z, H_x, H_y, H_z. Фрагмент сетки Yee показан на (рис.1).

Все компоненты (E_x, E_y, E_z, H_x, H_y, H_z) находятся в разных местах, т.е. разнесены в пространстве. Е - компоненты находятся посередине ребер, Н - компоненты - по центру граней. Все компоненты независимы друг от друга, т.е. каждой из них можно присвоить свои уникальные электрические (для Е) и магнитные (для Н) параметры.

Пространственные координаты каждого вектора x, y и z выражаются в номерах ячеек i, j и k соответственно, время t выражается в шагах n по времени:

где ∆x, ∆y, ∆z - размеры пространственной ячейки, ∆t - шаг по времени.

Поля E и H вычисляются со сдвигом на полшага по времени. Обозначения, введенные Yee, следующие: Eⁿ - значение поля E на только что вычисленном шаге; Eⁿ⁺¹ - значение поля E на вычисляемом сейчас шаге по времени. H^n-1/2 - значение поля H на только что вычисленном шаге; H^n+1/2 - значение поля на вычисляемом сейчас полушаге по времени. Из этих обозначений следует, что процедура вычислений начинается с поля H^n+1/2, потому что в момент t=0 (n=0) установлены начальные условия по всему счетному объему: все значения полей E и H равны нулю. Хотя в принципе это лишь наиболее распространенная условность. Можно считать, что пространственная сетка проходит через вектора H, что процедура счета начинается с поля E.

Теперь, когда введены основные обозначения, покажем вывод выражений, пригодных для расчетов с помощью компьютера и которым уже 40 лет.

Поставим (3) и (2) в (1). Получим:

Применяя конечно-разностную аппроксимацию, преобразуем (5) в выражения для шагов n и n+1, учитывая (4). Получим:

Подставляя (6) в (5) и решая получившиеся выражения относительно Hy^n+1/2_{(i+1/2,j,k+1/2)} и Exⁿ⁺¹_(i+1/2,j,k) получим:

Аналогичные выражения можно получить для остальных четырех компонент ячейки Yee.

Из выражений (7) и (8) видно, что значения μ, ε и σ задаются для каждого их векторов ячейки и могут быть различными в разных направлениях. Т.е. при необходимости можно задать анизотропию материалов для Е и/или Н полей.

Выражения (7) и (8) являются достаточными для многих решаемых задач, но для расчетов сосредоточенных элементов (источников напряжения, индуктивностей, транзисторов и т.п.), а также для расчетов материалов с нелинейными свойствами требуется их модификация.

В заключение следует упомянуть, что явные конечно-разностные схемы требуют специальных условий для устойчивой работы. Для метода FDTD это условие имеет вид:

∆t ≤ 1/(v √((1/∆x²)+ (1/∆y²)+ (1/∆z²))),

где v - максимальная скорость электромагнитных волн в счетном объеме, а выражение (1/∆x²)+ (1/∆y²)+ (1/∆z²) находится под знаком квадратного корня.

Обычно v = c (скорости света в вакууме).