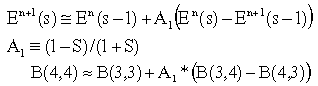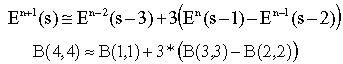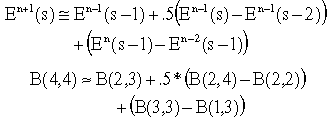Сайт Александра Зеленина

 

Александр Зеленин.

Граничные условия для FDTD.

В счетном объеме каждый вектор Е или Н вычисляется через 4 соседних вектора. Так происходит по всему объему. Но на границах самые последние векторы Е имеют: на гранях параллелепипеда счетного объема только три соседних вектора Н из четырех необходимых; на ребрах - два. Поэтому точно вычислить поле Е на границах невозможно.

Проблема вычисления граничных полей решается различными способами.

1. Условия PEC - идеальный проводник.

Условия PEC таковы, что граничные вектора Е никогда не вычисляются, а, значит, всегда равны нулю. Как известно, поле Е всегда равно нулю в идеальном проводнике, поэтому такие границы ведут себя как идеальный проводник: электромагнитные волны 100 % отражаются обратно в счетный объем.

2. Условия симметрии.

В некоторых случаях поле Е или поле Н может быть симметричным относительно некоторой плоскости. Тогда в этой плоскости можно задать условие симметрии и тем самым вдвое уменьшить счетный объем. При этом рядом с данной плоскостью симметрии будет проходить граница счетного объема с условиями симметрии.

Симметрия может быть четной или нечетной.

При нечетной симметрии плоскость симметрии проходит внутри счетного объема параллельно грани на расстоянии пол-ячейки от грани. Условия нечетной симметрии для симметрии по Е получаются простым переносом значений ближайших к границе векторов Е на саму границу, а для симметрии по Н получаются так же, но при этом вектор Е меняет свой знак. Ниже приведены примеры нечетной симметрии для Е и Н.

Пример: нечетная симметрия по Е:

  // ПЛОСКОСТЬ Y=1/2 симметрична по E

          For I:=1 to NX-1 do

             For K:=1 to NZ do  EX[I,1,K]:=EX[I,2,K];

          For I:=1 to NX do

             For K:=1 to NZ-1 do  EZ[I,1,K]:=EZ[I,2,K];

Пример: нечетная симметрия по Н:

  // ПЛОСКОСТЬ Y=1/2 симметрична по H

          For I:=1 to NX-1 do

             For K:=1 to NZ do  EX[I,1,K]:=-EX[I,2,K];

          For I:=1 to NX do

             For K:=1 to NZ-1 do  EZ[I,1,K]:=-EZ[I,2,K];

Условия четной симметрии несколько сложнее. Плоскость симметрии проходит на расстоянии целой ячейки от границы, поэтому кроме поля Е на границе необходимо помнить о прилегающих к границе векторах Н. При этом симметрии по Е и Н отличаются друг от друга только знаками переносимых значений.

Пример: четная симметрия по Н:

  // ПЛОСКОСТЬ Y=1 симметрична по H, вычисление поля Е

     begin

         For K:=1 to NZ do

            For I:=1 to NX-1 do   EX[I,1,K]:=-EX[I,3,K];

         For K:=1 to NZ-1 do

            For I:=1 to NX do     EZ[I,1,K]:=-EZ[I,3,K];

     end;

  // ПЛОСКОСТЬ Y=1 симметрична по H, вычисление поля Н

     begin

         For K:=1 to NZ-1 do

            For I:=1 to NX do   HX[I,1,K]:=HX[I,2,K];

         For K:=1 to NZ do

            For I:=1 to NX-1 do     HZ[I,1,K]:=HZ[I,2,K];

     end;                 

Пример: четная симметрия по Е:

  // ПЛОСКОСТЬ Y=1 симметрична по Е, вычисление поля Е

     begin

         For K:=1 to NZ do

            For I:=1 to NX-1 do   EX[I,1,K]:=EX[I,3,K];

         For K:=1 to NZ-1 do

            For I:=1 to NX do     EZ[I,1,K]:=EZ[I,3,K];

     end;

  // ПЛОСКОСТЬ Y=1 симметрична по Е, вычисление поля Н

     begin

         For K:=1 to NZ-1 do

            For I:=1 to NX do   HX[I,1,K]:=-HX[I,2,K];

         For K:=1 to NZ do

            For I:=1 to NX-1 do     HZ[I,1,K]:=-HZ[I,2,K];

     end;                 

При четной симметрии граничные поля Е и Н устанавливаются не одновременно, а на соответствующих полушагах по времени.

3. Простые условия поглощения (АВС)

Для условий поглощения значения векторов электрического поля на границе вычисляются на основании известных полей в приграничных слоях. Причем берутся приграничные поля не только на текущем шаге по времени, но и на предыдущих шагах. Все эти условия пытаются спрогнозировать поле на границе.

В литературе встречается описание целого ряда простых условий поглощения разных авторов. Всего их наберется с десяток. Практически чаще всего применяют условия Мура (Mur) и Лиао (Liao). Остальные не применяют или используют очень редко из-за их более низкой эффективности (Trefethen-Halpern, Higdon) или неудобства в использовании (Retarded Time - RT), или из-за неприменимости в декартовых координатах (Bayliss-Turkel), или из-за тенденции к потере стабильности (относится почти ко всем условиям, но особо - к условиям, основанным на высших порядках точности конечных разностей).

Все условия имеют довольно низкий коэффициент отражения от границы, составляющий порядка 0,1..1 %, но только при падении волны на границу под прямым углом. При падении под острым углом коэффициент отражения растет вплоть до 100 % при падении по касательной. Из-за этого границы необходимо располагать как можно дальше от источника электромагнитных волн, чтобы волны приходили к границе под как можно большими углами, желательно по нормали к границе.

Следует отметить, что оценка эффективности тех или иных простых граничных условий различна у разных авторов. Например, один источник пишет, что условия Лиао на 20 dB эффективнее условий Мура 2-го порядка. Другой пишет, что условия Лиао на 12 dB хуже условий Мура 1-го порядка. Имеется ввиду коэффициент отражения. И оба доказывают свои выводы графиками сравнительных расчетов.

Истина, скорее всего, посередине: для каждой конкретной задачи имеются свои оптимальные граничные условия. Одно плохо - заранее никогда не знаешь, КАКИЕ лучше.

Примечание. Возможно, введение чисел двойной точности радикально повысит стабильность, но пока это непозволительная роскошь, расходующая в два раза больше памяти и времени.

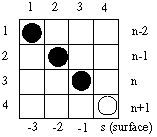
Итак, граничных условий много. Здесь рассмотрим три варианта простейших граничных условий: Мура 1-го порядка, Лиао 3-го порядка и RT. В таблице S (большое) и s (малое) - разные переменные! S = (dT * c)/ D - число Куранта, где D - шаг по пространству, dT- шаг по времени, с- скорость света, а s - координата границы. s-1 - одна ячейка внутрь счетного объема, s-2 - две ячейки от границы и т.д. На поясняющих рисунках от границы (surface - внешней поверхности счетного объема) по горизонтали отложена координата s, а по вертикали - время в шагах счета (n - временной индекс). Формула приведена в двух видах, дополняющих друг друга в пространстве и времени. На рисунках пустой кружок - вычисляемое значение, черные кружки - требуемые значения. Сразу можно определить, какие переменные приграничной области нужно хранить в дополнительных массивах и сколько шагов по времени они должны храниться.

Условия	Формула	Поясняющая картинка
Mur 1-го порядка	типично S=0,5 для минимального отражения под прямым углом, но может меняться для получения минимального коэффициента отражения под другими углами.
Liao 3-го порядка	Для данного случая S=0,5. Примечание: в литературе условия Лиао часто ставят особняком с условиями ABC, т.к. они базируются на других исходных предпосылках.
RT-ABC	Для данного случая S=0,5, шаг по времени строго полшага по пространству*, шаг по пространству строго одинаков во всех направлениях.

*Когда речь идет о сопоставлении времени и размеров пространства, то, конечно, секунды с метрами не сравниваются. Время превращается в расстояние при умножении на скорость. В данном случае шаг по времени умножается на скорость света в вакууме и результат сравнивается с шагом по пространству: (dT c) = 0,5 D или, иначе, dT = 0,5 D/ c.

 

Видно, что больше всего массивов переменных нужно хранить для условий RT (5), меньше всего - для условий Мура (1). Для условий Лиао нужно 3 дополнительных массива переменных.

 

А теперь пример реализации условий Мура 1-го порядка.

Procedure MursFirstABC;

  var I,J,K: Integer;

begin

// УСЛОВИЯ ПОГЛОЩЕНИЯ. Массивы вида EZX1, EZXN и т.п. - массивы сохраненных на предыдущем шаге по времени значений поля Е в приграничной области. Процедура сохранения приводится ниже.

// коэффициенты Tx, Ty и Tz равны c*dT/dX, c*dT/dY и c*dT/dZ соответственно. c-скорость света, dT- шаг по времени; dX, dY, dZ - шаги по пространству.

 

  //ЛЕВАЯ И ПРАВАЯ ПЛОСКОСТИ

 // Ez для двух плоскостей YxZ (левой и правой)

      for J:=2 to NY-1 do

      for K:=1 to NZ-1 do begin

                EZ[1,J,K]:=EZX1[J,K]+(Tx-1)/(Tx+1)*(EZ[2,J,K]-EZ[1,J,K]);

                EZ[NX,J,K]:=EZXN[J,K]+(Tx-1)/(Tx+1)*(EZ[NX-1,J,K]-EZ[NX,J,K]);

      end;

 // Ey для двух плоскостей YxZ [левой и правой]

      for J:=1 to NY-1 do

      for K:=2 to NZ-1 do begin

             EY[1,J,K]:=EYX1[J,K]+(Tx-1)/(Tx+1)* (EY[2,J,K]-EY[1,J,K]);

           EY[NX,J,K]:=EYXN[J,K]+(Tx-1)/(Tx+1)* (EY[NX-1,J,K] -EY[NX,J,K]);

      end;

 

  //ВЕРХНЯЯ И НИЖНЯЯ ПЛОСКОСТИ

 // Ex для двух плоскостей XxZ [верхней и нижней]

      for K:=2 to NZ-1 do

      for I:=1 to NX-1 do begin

             EX[I,1,K]:=  EXY1[I,K]+(Ty-1)/(Ty+1)*(EX[I,2,K]-EX[I,1,K]);

             EX[I,NY,K]:=  EXYN[I,K]+(Ty-1)/(Ty+1)*(EX[I,NY-1,K]-EX[I,NY,K]);

      end;

 

 // Ez для двух плоскостей XxZ [верхней и нижней]

      for K:=1 to NZ-1 do

      for I:=2 to NX-1 do begin

             EZ[I,1,K]:=  EZY1[I,K]+(Ty-1)/(Ty+1)*(EZ[I,2,K]-EZ[I,1,K]);

             EZ[I,NY,K]:=  EZYN[I,K]+(Ty-1)/(Ty+1)*(EZ[I,NY-1,K]-EZ[I,NY,K]);

      end;

 

  //БЛИЖНЯЯ И ДАЛЬНЯЯ ПЛОСКОСТИ

 // Ey для двух плоскостей XxY [ближней и дальней]

      for I:=2 to NX-1 do

      for J:=1 to NY-1 do begin

              EY[I,J,NZ]:=EYZN[I,J]+(Tz-1)/(Tz+1)*(EY[I,J,NZ-1]-EY[I,J,NZ]);

              EY[I,J,1]:=EYZ1[I,J]+(Tz-1)/(Tz+1)*(EY[I,J,2]-EY[I,J,1]);

      end;

 

 // Ex для двух плоскостей XxY [ближней и дальней]

      for I:=1 to NX-1 do

      for J:=2 to NY-1 do begin

            EX[I,J,NZ]:=  EXZN[I,J]+(Tz-1)/(Tz+1)*(EX[I,J,NZ-1]-EX[I,J,NZ]);

            EX[I,J,1]:=  EXZ1[I,J]+(Tz-1)/(Tz+1)*(EX[I,J,2]-EX[I,J,1]);

      end;

 

// РЕБРА, параллельные оси Z

      for K:=1 to NZ-1 do begin

                EZ[1,1,K]:=EZX1[1,K]+(Tx-1)/(Tx+1)*(EZ[2,1,K]-EZ[1,1,K]);

                EZ[1,NY,K]:=EZX1[NY,K]+(Tx-1)/(Tx+1)*(EZ[2,NY,K]-EZ[1,NY,K]);

                EZ[NX,1,K]:=EZXN[1,K]+(Tx-1)/(Tx+1)*(EZ[NX-1,1,K]-EZ[NX,1,K]);

                EZ[NX,NY,K]:=EZXN[NY,K]+(Tx-1)/(Tx+1)*(EZ[NX-1,NY,K]-EZ[NX,NY,K]);

      end;

 

// РЕБРА, параллельные оси Y

      for J:=1 to NY-1 do begin

               EY[1,J,1]:=EYX1[J,1]+(Tx-1)/(Tx+1)*(EY[2,J,1]-EY[1,J,1]);

               EY[1,J,NZ]:=EYX1[J,NZ]+(Tx-1)/(Tx+1)*(EY[2,J,NZ]-EY[1,J,NZ]);

               EY[NX,J,1]:=EYXN[J,1]+(Tx-1)/(Tx+1)*(EY[NX-1,J,1]-EY[NX,J,1]);

               EY[NX,J,NZ]:=EYXN[J,NZ]+(Tx-1)/(Tx+1)*(EY[NX-1,J,NZ]-EY[NX,J,NZ]);

      end;

 

// РЕБРА, параллельные оси X

      for I:=1 to NX-1 do begin

                 EX[I,1,1]:=EXY1[I,1]+ (Ty-1)/(Ty+1)*(EX[I,2,1]-EX[I,1,1]);

                 EX[I,1,NZ]:=EXYN[I,NZ]+(Ty-1)/(Ty+1)*(EX[I,2,NZ]-EX[I,1,NZ]);

                 EX[I,NY,1]:=EXY1[I,1]+(Ty-1)/(Ty+1)*(EX[I,NY-1,1]-EX[I,NY,1]);

                 EX[I,NY,NZ]:=EXYN[I,NZ]+(Ty-1)/(Ty+1)*(EX[I,NY-1,NZ]-EX[I,NY,NZ]);

      end;

end;

// сохранение приграничных полей для MursFirstABC

Procedure GetBorderValues;

  var I,J,K: Integer;

begin

     // слева и справа

      for J:=1 to NY do for k:=1 to NZ-1 do

          begin

          EZX1[J,K]:=EZ[2,J,K];

          EZXN[J,K]:=EZ[NX-1,J,K];

          end;

      for J:=1 to NY-1 do for k:=1 to NZ do

          begin

          EYX1[J,K]:=EY[2,J,K];

          EYXN[J,K]:=EY[NX-1,J,K];

          end;

     // верх и низ

      for I:=1 to NX do for k:=1 to NZ-1 do

          begin

          EZY1[I,K]:=EZ[I,2,K];

          EZYN[I,K]:=EZ[I,NY-1,K];

          end;

      for I:=1 to NX-1 do for k:=1 to NZ do

          begin

          EXY1[I,K]:=EX[I,2,K];

          EXYN[I,K]:=EX[I,NY-1,K];

          end;

     // ближняя и дальняя

      for I:=1 to NX do for J:=1 to NY-1 do

          begin

          EYZ1[I,J]:=EY[I,J,2];

          EYZN[I,J]:=EY[I,J,NZ-1];

          end;

      for I:=1 to NX-1 do for J:=1 to NY do

          begin

          EXZ1[I,J]:=EX[I,J,2];

          EXZN[I,J]:=EX[I,J,NZ-1];

          end;

end;

Примечание: в литературе встречается и несколько иная форма записи условий Мура 1-го порядка. К приведенной здесь формуле добавляется еще один член, который сам Мур относит к условиям второго порядка, а другие авторы утверждают, что этот член должен быть и в формуле 1-го порядка.

Далее об условиях PML.