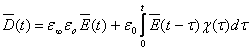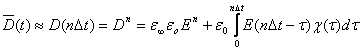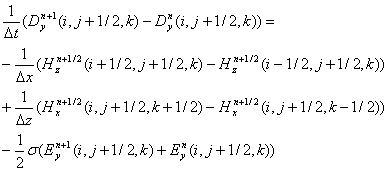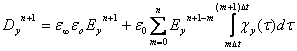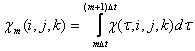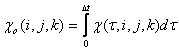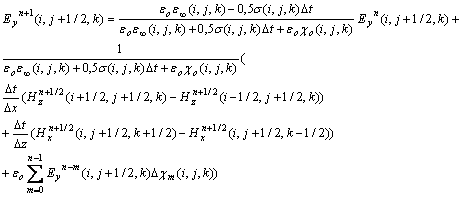Сайт Александра Зеленина
Применение метода FDTD для расчетов распространения нестационарных электромагнитных полей в условиях частотной дисперсии
Александр Зеленин
2003 г
Введение
В классической постановке [1] метод FDTD требует, чтобы значения проводимости и диэлектрической проницаемости материалов не зависели от частоты. В то же время, для многих материалов эти параметры имеют ярко выраженную частотную зависимость. К частотно-зависимым материалам относятся, в частности, биологические ткани и вода. Для биологических тканей в диапазоне частот от 40 МГц до 400 МГц диэлектрическая проницаемость уменьшается в 2-3 раза, проводимость возрастает также в 2-3 раза.
Если вычисления по методу FDTD проводятся для одной частоты, то можно задать значения проводимости и диэлектрической проницаемости материалов для конкретной частоты и этого обычно достаточно. Проблемы возникают тогда, когда необходимо провести численное моделирование взаимодействия широкополосных электромагнитных полей (например, коротких импульсов) c частотно-зависимыми материалами.
В [2] приводится частотно-зависимая формулировка (FD)2TD (frequency-dependent FDTD). Эта формулировка приведена с упрощениями, она не учитывает проводимости диэлектрика. Между тем, биологические ткани имеют существенную проводимость, которую следует учесть.
В [3] приводит новую формулировку (FD2)TD, в которой учитывается проводимость биологических тканей. К несчастью, эта формулировка в статье приведена с ошибками.
В настоящей статье приводится новая формулировка (FD2)TD для биологических тканей с учетом проводимости среды.
Учет проводимости биологических тканей в уравнениях (FD2)TD
Предположим, что биологические материалы линейные и изотропные, магнитная проницаемость является константой, не зависящей от частоты. Для этого случая в [2] приводится вывод уравнений без учета проводимости. Добавляя проводимость (это J в (1), см. ниже), повторим вывод уравнений.
Исходными являются уравнения Максвелла:
|
|
(1) |
|
|
(2) |
где 
, 
, 
-
удельная проводимость. Из уравнения (2) следует выражение для H, которое полностью совпадает с классической
формулировкой [1], поэтому вывод формулировки для Н в настоящей статье
не приводится.
Вектор
смещения 
из
(1) во временной области записывается как [2, 3]:
|
|
(3) |
где 
- диэлектрическая постоянная,
- относительная
диэлектрическая проницаемость на "бесконечной" частоте, 
- электрическая
восприимчивость.
Используя
обозначения, принятые в [1], запишем 
и для каждой компоненты векторов 
и 
в (3) можем записать:
|
|
(4) |
Уравнение (1)
с учетом того, что 
, 
и 
, 
в конечно-разностной дискретной форме в декартовых
координатах для компоненты 
имеет
вид:
|
|
(5) |
Принимая во
внимание, что 
и 
равны нулю при 
<0, можем записать (4) в виде:
|
|
(6) |
Выражение для
на следующем
временном шаге имеет вид:
|
|
(7) |
Подставляя выражения (6) и (7) в (5) получаем:
|
|
(8) |
Для удобства введем обозначения:
|
|
(9) |
Подставляя
(9) в (8) и решая последнее уравнение относительно 
, получаем:
|
|
(10) |
Выражения для
компонент 
и 
могут быть получены аналогичным
образом.
Если
относительная диэлектрическая проницаемость не зависит от частоты, то 
для всех m и 
=0.
В этом случае выражение (10) совпадает с [1].
Для полярных диэлектриков комплексная диэлектрическая проницаемость определяется как (формула Дебая):
|
|
(11) |
,где 
- комплексная диэлектрическая
проницаемость, зависящая от частоты.
Фурье-
преобразование функции 
имеет
вид:
,
где 
- функция, зависящая от
шага по времени.
Так как 
имеем:
Выражение
(10) содержит член 
, который, на первый взгляд, для
вычисления требует хранения большого количества переменных. Но, поскольку
функция носит экспоненциальный характер, то,
как показано в [2], определяя, что 
можем записать:
|
|
(12) |
Таким
образом, для каждой компоненты 
, 
и
требуется только
одна переменная.
Программная реализация алгоритма (FD2)TD
Здесь
приводится программный код, в котором вычисляется Е- поле по формуле (10), а
также обновляется значение для 
по формуле (12). Код написан на языке
Паскаль.
// Процедура определения электрического поля в одном шаге по времени
Procedure TimeStepForEBio;
var I,J,K: Integer;
begin
// вычисление X-компоненты
for I:=1 to XSize-1 do
for J:=2 to YSize-1 do
for K:=2 to ZSize-1 do
begin
EX[I,J,K]:=EX[I,J,K]*AE[I,J,K]+((HZ[I,J,K]-HZ[I,J-1,K])*TY-
(HY[I,J,K]-HY[I,J,K-1])*TZ+Eps0*PsiX[I,J,K])*BE[I,J,K];
PsiX[I,J,K]:=EX[I,J,K]*Delchi[i,j,k]+PsiX[I,J,K]*Expo[i,j,k];
end;
// вычисление Y-компоненты
for I:=2 to XSize-1 do
for J:=1 to YSize-1 do
for K:=2 to ZSize-1 do begin
EY[I,J,K]:=EY[I,J,K]*AE[I,J,K]+((HX[I,J,K]-HX[I,J,K-1])*TZ-
(HZ[I,J,K]-HZ[I-1,J,K])*TX+Eps0*PsiY[I,J,K])*BE[I,J,K];
PsiY[I,J,K]:=EY[I,J,K]*Delchi[i,j,k]+PsiY[I,J,K]*Expo[i,j,k];
end;
// вычисление Z-компоненты
for I:=2 to XSize-1 do
for J:=2 to YSize-1 do
for K:=1 to ZSize-1 do begin
EZ[I,J,K]:=EZ[I,J,K]*AE[I,J,K]+((HY[I,J,K]-HY[I-1,J,K])*TX-
(HX[I,J,K]-HX[I,J-1,K])*TY+Eps0*PsiZ[I,J,K])*BE[I,J,K];
PsiZ[I,J,K]:=EZ[I,J,K]*Delchi[i,j,k]+PsiZ[I,J,K]*Expo[i,j,k];
END;
end;// конец определения электрического поля
В данной
процедуре XSize, YSize,
ZSize - размер счетного
объема в количестве пространственных шагов по каждому измерению. EX, EY, EZ - вычисляемые компоненты электрического поля. HX, HY, HZ - вычисленные ранее компоненты магнитного поля. Eps0 - диэлектрическая постоянная. PsiX,
PsiY, PsiZ -
значения функции (12), Delchi и
Expo - 
и 
соответственно. TX,
TY, TZ -
коэффициенты, равные Dt/Dx, Dt/Dy и Dt/Dz - отношение шага
по времени к шагу по пространству.
Коэффициенты AE и ВE вычисляются один раз перед началом счета:
AE[i,j,k]:=(EPSInf[i,j,k]-SIG[i,j,k]*dT*0.5)/(EPSInf[i,j,k]+Xo[i,j,k]+SIG*DT*0.5);
BE[i,j,k]:=1.0/(EPSInf[i,j,k]+Xo[i,j,k]+SIG[i,j,k]* DT*0.5);
Здесь EPSInf =,SIG =, DT - шаг по времени, Xo = .
Процедура TimeStepForEBio легко встраивается в уже готовую программу, в которой был реализован алгоритм Yee простой заменой старой процедуры и подготовкой дополнительных массивов перед началом счета. При этом объем требуемой оперативной памяти возрастает примерно на 40 %, скорость вычислений снижается в 1,5 раза. Эти затраты окупаются возможностью более точного моделирования взаимодействия импульсных электромагнитных полей с дисперсионными средами.
Литература
1. Yee, K. S.: "Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media." IEEE Transactions on Antennas and Propagation, Vol. 14, No. 3, 1966, pp. 302-307.
2. Luebbers R. et all.: "A frequency-depended finite-difference time-domain formulation for dispersive materials." IEEE Transactions on Electromagnetic Compatibility, Vol. 32, No. 3, Aug. 1990, pp. 222-227.
3. Sullivan D. M.: "A frequency-depended FDTD Method for Biological Applications." IEEE Transactions on Microwave Theory and Techniques, Vol. 40, No. 3, March 1992, pp. 532-539.
файл:/zfdtd/method/pd.htm