На этой страничке находятся дополнительные сведения по методу расчета, которые не вошли в другие разделы сайта и вряд ли вообще встречаются в литературе по FDTD

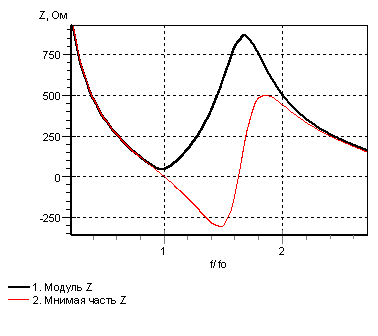
7. Как вычислить сопротивление в точке питания антенны?

Допустим, источником сигнала на входе антенны служит резистивный источник напряжения (РИН). В нем задается некое напряжение. Выводится ток через РИН и напряжение на нем (не то, которое задано, а то, которое получается в ячейке с РИН).

Для синусоидального сигнала. Нужно амплитуду напряжения на входе антенны разделить на амплитуду тока.

Для импульсного сигнала. Нужно спектр напряжения на входе антенны разделить на спектр тока.

На рисунке приведен пример вычисления сопротивления диполя с изогнутыми под 90 градусов концами. Отношение длины загнутой части плеча диполя к общей длине плеча равно 0,4. На графике fо – резонансная частота (полуволновой резонанс). Отношение длины диполя к диаметру равно 80

Мнимая часть Z используется для определения резонансной частоты. Там, где она равна нулю и есть резонанс. В данном случае на частоте резонанса сопротивление диполя около 51 Ом.

Примечание. Приведенный выше график похож, но не совпадает по горизонтали с графиками зависимости характеристик вибраторов от вида резонанса (полуволновой, волновой и т.п.) в литературе по теории антенн. Это нормально, т.к. мы привели характеристику реального, «толстого» вибратора, а не бесконечно тонкого.

8. При моделировании антенн иногда результат вычислений получается со значительными ошибками. Резонансная частота получается ниже даже с учетом коэффициента укорочения антенны, а поле вдали от антенны получается больше. В чем причина?

Причина кроется в свойствах ячейки Yee. В литературе часто пишут, что из-за цифровой дисперсии и анизотропии алгоритма протяженные проводящие структуры имеют несколько большую длину, чем мы задаем. Но мне не встретилась количественная оценка этой длины. Я исследовал этот вопрос с помощью решения двух задач: зависимость сопротивления вибратора от частоты (см. предыдущий ответ) и расчет поля на значительном удалении от вибратора.

Оказалось, что решение лучше совпадает с аналитическим решением, если со всех сторон к вибратору мысленно прибавить по полшага по пространству. Например, вибратор длиной 10 ячеек на самом деле имеет длину ~11 ячеек, а при толщине в 1 ячейку (когда заданы все 4 вектора Е в одном направлении) реальная толщина приблизительно равна двум ячейкам.

Хорошо видимое различие между задаваемой и реальной длиной можно получить, если решить задачу вычисления поля в дальней зоне от элементарного электрического диполя. Зададим диполь из одного источника напряжения. При шаге по пространству в 1 см может показаться, что длина диполя составляет 1 см. Для такого диполя при возбуждении его током в 1 А на частоте 300 МГц и на расстоянии 4 м при расчете по аналитическим формулам, например, в частотной области:

при угле под синусом 90 градусов поле должно быть 0,47 В/м. А при вычислениях FDTD получаем поле ~0,74 В/м. Разницу в 1,57 раза можно объяснить тем, что длина диполя на самом деле не 1 см, а 1,57 см.

Аналогично для диполя из двух источников (длина = 2 ячейки по 1 см) получаем реальную длину 2,5 см.

Однако, при моделировании диполя тремя последовательными источниками напряжения результат получается точным: длина ровно 3 ячейки, для 4-х источников длина составляет 3,8 ячейки. Для трех и более ячеек данный способ тестирования не подходит, т.к. уже перестает быть «элементарным» и приведенная выше формула уже не дает правильный результат (распределение тока по длине диполя перестает быть равномерным.)