Сайт Александра Зеленина

Применение метода FDTD для вычисления электромагнитных полей в дальней зоне

Деление вычислительного объема на области полного и рассеянного поля

Александр Зеленин

2006 г

Когда источники электромагнитного поля находятся внутри вычислительной области, то вычисление дальнего поля можно применять, окружив все источники поля и рассеивающие объекты единой поверхностью интегрирования. Но если задается поле от внешнего источника, который находится за пределами вычислительной области, то требуется сделать так, чтобы на поверхности интегрирования не было поля от внешнего источника, а присутствовало только рассеянное поле.

Когда задается внешнее поле, то, в принципе, нам известно движущееся поле в любой момент времени и в любой точке свободного пространства вычислительной области. Этим знанием можно воспользоваться, чтобы разделить вычислительную область на две части: внутреннюю, где присутствует полное поле, т.е. сумма падающего и рассеянного полей, и наружную, где существует только рассеянное поле (рис. 1).

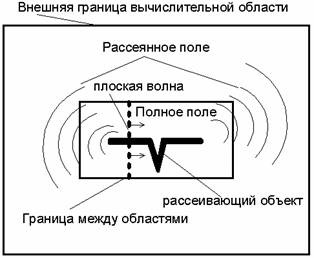
Рис. 1.

Способ задания полей на границе раздела приведен в [1,2] для двумерного случая. Здесь этот способ рассмотрен более подробно. Основная идея заключается в том, что в вычислительной области задается объект обычным для метода FDTD способом - заданием электрофизических характеристик в ячейках. Этот объект окружается границей, на которой задается падающее поле, как показано на рис. 1. Внутри границы получается регион полного поля, снаружи – рассеянного. На другой, внешней, границе вычислительного объема выполняются граничные условия излучения, например, условия Мура [3] или PML [4].

Рассмотрим фрагмент сетки, внутри которого находится граница полного/рассеянного поля. Примем, что граница области полного поля проходит по векторам электрического поля, а занимает эта область всего одну кубическую ячейку. Граница проходит по граням ячейки. На рис. 2 изображена данная ситуация. Все четыре вектора E, показанные на рис. 2, окружают регион полного поля и входят в него. Остальные восемь векторов Е этой ячейки не показаны, чтобы не загромождать рисунок, но подразумевается, что они находятся на ребрах ячейки, уходящих вглубь рисунка. Если на каждом вычислительном шаге (при вычислении поля Е) просто добавлять к векторам E на границе падающее поле (напомним, что падающее поле нам известно заранее для всех компонентов во всех точках пространства), то на следующем шаге это приведет к тому, что соседние векторы Н изменят свои значения. Изменятся те векторы Н, которые создают вихрь вокруг граничных векторов E. Часть из них принадлежит области полного поля. Но нам нужно, чтобы поле Н снаружи от границы не менялось и не реагировало на падающее поле. Поэтому нужно вычесть из векторов Н снаружи от границы тот вклад, который был внесен падающим полем.

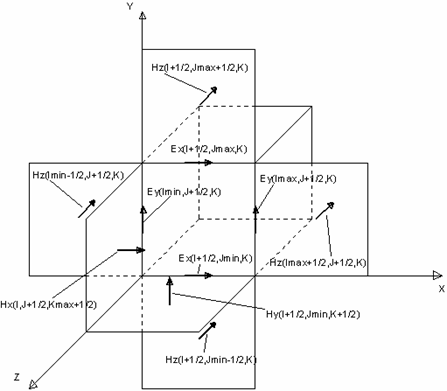
Рис. 2.

Поле Е на границе добавляется по принципу:

Eⁿ⁺¹_{полное
на границе} = Eⁿ⁺¹_{полученное
из обычного алгоритма}-K1 Hⁿ^+1/2_{падающее
снаружи от границы}

Поле Н снаружи от границы восстанавливается по принципу:

Н^n+1/2_{снаружи от
границы} = Н^n+1/2_{полученное из
обычного алгоритма}-K2 Eⁿ_{падающее
на границе}

Здесь K1 и K2 – коэффициенты, аналогичные коэффициентам обычного алгоритма. В простейшем случае K1= Δt/(ε Δ); K2= Δt/(μ Δ), где Δ – шаг сетки.

Такая процедура не требует изменения существующего алгоритма, а лишь дополняет его. Обозначим через Imin, Imax, Jmin, Jmax, Kmin, Kmax – индексы сетки, ограничивающие область полного поля и примем, что поле движется вдоль положительного направления оси X, вектор Е направлен по оси Y, а вектор H – по оси Z. Также будем считать, что обычная процедура вычисления поля Hⁿ^+1/2 уже выполнена.

Тогда на левой границе (согласно рис. 2) для всех Hz:

Hzⁿ^+1/2₍_Imin-1/2,_J+1/2,_K)= Hzⁿ^+1/2₍_Imin-1/2,_J+1/2,_K)+Δt/(μ Δx) Eyⁿ_{падающее
(}_Imin,_J+1/2,_K)

На правой границе для всех Hz около границы:

Hzⁿ^+1/2₍_Imax+1/2,_J+1/2,_K)= Hzⁿ^+1/2₍_Imax+1/2,_J+1/2,_K)-Δt/(μ Δx) Eyⁿ_{падающее
(}_Imax,_J+1/2,_K)

На дальней границе для всех Hx около границы:

Hxⁿ^+1/2₍_I,_J+1/2,_K_min-1/2)= Hzⁿ^+1/2₍_I,_J+1/2,_K_min-1/2)-Δt/(μ Δz) Eyⁿ_{падающее
(}_I,_J+1/2,_Kmin)

На дальней границе для всех Hx около границы:

Hxⁿ^+1/2₍_I,_J+1/2,_K_max+1/2)= Hzⁿ^+1/2₍_I,_J+1/2,_K_min-1/2)+Δt/(μ Δz) Eyⁿ_{падающее
(}_I,_J+1/2,_Kmах)

Так как нет компонент Ex и Ez, что было условлено выше, то другие составляющие поля H на границе не требуют дополнительных вычислений. В случае наличия Ex и Ez выражения для остальных компонентов поля H на границе составляются аналогично приведенным выше.

Для электрического поля (в рассматриваемом случае поле содержит только Ey и Hz компоненты) требуется учет падающего поля не только для компоненты Ey, но и для Ex. После обычной процедуры вычисления поля Eⁿ⁺¹ на левой границе для всех Ey:

Eyⁿ⁺¹₍_Imin,_J+1/2,_K)= Eyⁿ⁺¹₍_Imin,_J+1/2,_K)+Δt/(ε Δx) Hzⁿ^+1/2_{падающее
(}_Imin-1/2,_J+1/2,_K)

На правой границе для всех Ey:

Eyⁿ⁺¹₍_Imax,_J+1/2,_K)= Eyⁿ⁺¹₍_Imax,_J+1/2,_K)-Δt/(ε Δx) Hzⁿ^+1/2_{падающее
(}_Imax+1/2,_J+1/2,_K)

На нижней границе для всех Ex:

Exⁿ⁺¹₍_I+1/2,_Jmin,_K)= Exⁿ⁺¹₍_I+1/2,_Jmin,_K)-Δt/(ε Δy) Hzⁿ^+1/2_{падающее
(}_I+1/2,_J_min-1/2,_K)

На верхней границе для всех Ex:

Exⁿ⁺¹₍_I+1/2,_Jmax,_K)= Exⁿ⁺¹₍_I+1/2,_Jmax,_K)+Δt/(ε Δy) Hzⁿ^+1/2_{падающее
(}_I+1/2,_J_min+1/2,_K)

Для задания других направлений падения волны следует поступать аналогично рассмотренному случаю.

Выше приведено только 8 уравнений. Всего может быть до 24 уравнений: 12 для поля E на границе и 12 для поля H снаружи от границы. При этом необходимо внимательно следить за расстановкой знаков перед слагаемым с падающим полем.

Литература

1. K. R. Umashankar and A. Taflove, “A novel method to analyze electromagnetic scattering of complex objects”: IEEE Trans. Electromagn. Compat., vol. 24, pp. 397–405, 1982.

2. I. Wayan Sundiarta, “An Absording Boundary Condition for FDTD Truncation Using Multiple Absorbing Surfaces”: IEEE Trans. On Antennas and Propag., vol. 51, pp. 3268–3275, December 2002.

3. G. Mur, “Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations”: IEEE Trans. Electromagn. Compat. EMC-23, 377 (1981).

4. Berenger, J. P., “A perfectly matched layer for the absorption of electromagnetic waves”: J. Comput. Phys., 114, 185–200, 1994.

файл:/zfdtd/method/tfsf.htm