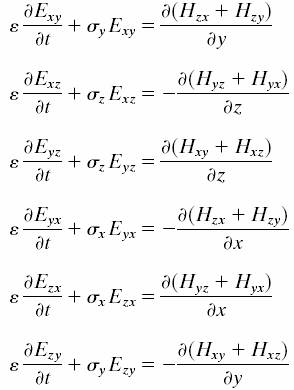Сайт Александра Зеленина
Александр Зеленин.
Граничные условия для FDTD (продолжение).
4. Условия PМL - идеально сочетающиеся слои.
Примечание. Вообще-то, дословный перевод "Perfectly Matched Layer" выглядит как "идеально согласованный (сочетающийся) слой". Но, во-первых, по одному слою в этих граничных условиях не применяют, а, во-вторых, если один слой с чем-то сочетается, то, несомненно, с другим слоем. То есть их минимум два, а значит, по-русски, множественное число – "слои".
Условия PML впервые опубликованы в статье [J. P. Berenger, JOURNAL OF COMPUTATIONAL PHYSICS. 114, 185 (1994)], а затем получили развитие в публикациях этого автора в 1995-1996 г. При возникновении интереса к безусловно-стабильным алгоритмам (для тех, кто еще не знаком, есть такие алгоритмы, которые не обременены условием Куранта и появились в конце 20 века) рядом авторов были разработаны условия PML, адаптированные к новым алгоритмам.
Условия PML обладают низким коэффициентом отражения (по некоторым данным в миллион раз меньше, чем у условий Мура), а также практической независимостью от угла падения волны.
К недостаткам условий PML следует отнести значительно больший объем требуемой памяти, чем для условий ABC и наличие нижней граничной частоты, для снижения которой требуется увеличения количества слоев PML, а, следовательно, требуемой памяти. Как следствие увеличения требуемого объема памяти происходить снижение скорости вычислений.
За пределами главного счетного объема добавляются дополнительные ячейки, окружающие счетный объем по периметру несколькими слоями. Электрическое и магнитное поле в этих ячейках вычисляется почти так же, как и в счетном объеме, но есть отличия.
Во-первых, в уравнения в обязательном порядке вводятся электрические и магнитные потери. В главном алгоритме этих потерь может не быть вообще. В уравнениях главного алгоритма >(рис. 2) учтены только электрические потери. Магнитные потери вводятся так же, как и электрические, путем задания "плотности магнитных токов". Тогда уравнения Максвелла (1) и (2) выглядят так:
|
rot(H) = ∂D/∂t + J; rot(E) = - ∂B/∂t + J*; |
(9) |
где
|
D = ε εo E; J = σ E; B = μ μo H; J* = σ* H; |
(10) |
Отличие от (1) и (2) только в появлении J* - плотности "магнитных токов" и σ* - "магнитной проводимости". С введением магнитных потерь уравнения (9) стали симметричными.
Во-вторых, вводится разделение векторов и их раздельное вычисление. Каждый вектор декартовой сетки Yee в границах PML делится на два параллельных вектора (две компоненты). Сумма этих векторов есть полный вектор: Eх = Exy + Exz; Ey = Eyx + Eyz; Hz = Hzx + Hzy и т.д. Обозначения расшифровываются так: Exy - вектор E в направлении X, полученный через соседние векторы Hz, лежащие на прямой, параллельной оси Y. Понять это можно, посмотрев на систему уравнений Беренгера:
Примечание. Схему Беренгера называют «раздельной», т.к. вводится разделение векторов. Есть также предложения других авторов применять «нераздельную» схему. Если кто-нибудь проверял работу «нераздельной» схемы, поделитесь впечатлениями. Я не доверяю автору «нераздельной» схемы из-за целого ряда некорректных статей за его авторством, а также авторством его учеников и соратников. Сложилось впечатление, что некий клан печет статьи как пирожки не придавая внимания содержанию – лишь бы побольше опубликовать. Буду рад, если мое впечатление ошибочно.
|
|
|
(11) |
В третьих, теоретически, если выполняется условие
|
σi/ εo = σi*/ μo, |
(12) |
то на границе раздела двух сред скорость электромагнитных волн не изменяется и отражение рано нулю. В то же время, поскольку σi и σi* не равны нулю, то происходит поглощение электромагнитных волн в недрах PML.
К сожалению, отражение все же есть:
- от первого слоя PML;
- между слоями PML, поскольку для экономии вычислительных ресурсов потери растут от слоя к слою (закон изменения потерь от первого слоя к последнему называется "профилем потерь");
- после последнего слоя PML, поскольку там находится PEC - граница.
Отражение от первого слоя PML и между слоями PML вызвано ошибками конечно-разностной дискретизации, и, в первую очередь, тем, что векторы E и H (а, следовательно, σi и σi*) не совпадают в пространстве. Для снижения отражения внутри PML необходимо ограничивать скорость роста потерь некоторым разумным пределом.
Беренгер показал, что при каждом конкретном значении σi и σi*, вследствие цифрового отражения, происходит отражение нормальных (перпендикулярных) к границе электромагнитных волн, частота которых ниже fc (частота отсечки). Чем больше σi и σi*, тем выше fc. Поэтому при проникновении волны в границы PML вначале идет отражение от первого слоя с проводимостью σ0 тех частот, которые ниже fc0. Затем идет отражение от полуслоя с проводимостью σ0* частот ниже fc0*. Причем fc0 < fc0*. И так далее – все более и более высокие частоты отражаются, причем отражение от σi и от σi*.
Отражение от PEC границы после последнего слоя PML происходит обычно уже для весьма ослабленной волны. Отраженная волна на обратном пути продолжает ослабляться. Но если слоев мало (обычно < 5), то отраженная волна может быть существенной.
Для уменьшения отражения от первого слоя значения σ1 специально выбирается маленьким. Для уменьшения отражения между слоями профиль потерь выбирается с ограниченной скоростью роста потерь. Для уменьшения влияния волны, отраженной от РЕС границы, увеличивается количество слоев PML.
Как вариант, Беренгер предлагает следующий геометрический профиль потерь:
|
|
(13) |
где g - коэффициент геометрической прогрессии; Dx - шаг по пространству; с - скорость света; N - номер PML -слоя, считая от интерфейса счетного региона и границы; r - расстояние от границы; R(0) - коэффициент отражения от первого слоя. Рекомендуемое значение R(0) =0.01 (1 %) Коэффициент прогрессии g рекомендуется брать 2,15. Это значение получено Беренгером экспериментально, хотя встречаются и другие рекомендации.
σ*(r) получается через σ(r) с использованием (12).
На низких частотах наблюдается резкое увеличение коэффициента отражения от границ PML. Нижняя граничная частота отсечки для известного значения электрической проводимости на границе находится из выражения:
|
|
(14) |
Для расчетов откликов от импульсов - ступенек с постоянной составляющей обратная величина к (14) - 1/fc - это максимальное время счета, при котором коэффициент отражения от первого слоя еще не превышает заданного R(0).
На самом деле, fc полученное по (14), - сильно заниженное значение. Реально происходят отражения и от других слоев, которые, как указано выше, имеют более высокую частоту отсечки. Практически fc нужно брать в 5 раз больше, что показывается в разделе сравнение граничных условий.
Существуют и другие профили потерь. В статье Беренгера "PML for the FDTD Solution of Wave-Structure Interaction Problems" (IEEE trans. on antennas and prop., vol. 44, N1, Jan 1996) есть богатый материал для размышлений о выборе профиля потерь и количества слоев в зависимости от разных факторов.
Дискретизация уравнений (11) происходит так же, как и дискретизация уравнений главного алгоритма. Для двух векторов Ex:
Exyn+1(i+1/2,j,k) = (1-0,5 σy(r)∆t)/ (1+0,5 σy(r)∆t) Exyn(i+1/2,j,k) +
∆t/ (1+0,5 σy(r)∆t)/ ∆y (Hzxn+1/2(i+1/2,j+1/2,k) + Hzyn+1/2 (i+1/2,j+1/2,k) -
Hzxn+1/2(i+1/2,j-1/2,k) - Hzyn+1/2 (i+1/2,j-1/2,k))
Exzn+1(i+1/2,j,k) = (1-0,5 σz(r)∆t)/ (1+0,5 σz(r)∆t) Exzn(i+1/2,j,k) +
∆t/ (1+0,5 σz(r)∆t)/ ∆z (Hyxn+1/2(i+1/2,j,k+1/2) + Hyzn+1/2 (i+1/2,j,k+1/2) -
Hyxn+1/2(i+1/2,j,k-1/2) - Hyzn+1/2 (i+1/2,j,k-1/2))
Для остальных векторов Е все аналогично. Для векторов Н уравнения аналогичные, но вместо σ(r) берется σ*(r).
Hxyn+1/2(i,j+1/2,k+1/2) = (1-0,5 σ*y(r)∆t)/ (1+0,5 σ*y(r)∆t) Hxyn-1/2 (i,j+1/2,k+1/2) -
∆t/ (1+0,5 σ*y(r)∆t)/ ∆y (Ezxn(i,j+1,k+1/2) + Ezyn (i,j+1,k+1/2) -
Ezxn(i,j,k+1/2) - Ezyn (i,j,k+1/2))
Как можно заметить, в уравнениях для векторов Е имеются суммы типа (Hzxn+1/2(i+1/2,j+1/2,k) + Hzyn+1/2 (i+1/2,j+1/2,k)). Это и есть полный вектор, в данном случае Hz. Когда вычисляется поле на границе счетного объема, то из счетного объема берется полный вектор Hz, а из граничного PML-слоя – сумма Hzx+ Hzy. Также и для других векторов.
На внешней границе PML, как уже говорилось, тангенциальные векторы Е равны нулю (PEC).
Профиль потерь зависит только от координаты, ведущей от интерфейса "счетный объем" - PML вглубь PML. На любой грани прямоугольного счетного объема вглубь PML ведет только одна координата. Допустим, это координата X. Тогда σx(r) меняется по заданному закону, а σy(r) = σz(r) = 0. На ребрах вглубь PML ведут уже две координаты (одна из σ равна нулю), а в углах вглубь ведут все три координаты и, следовательно, изменяются все σ (рис. 1).
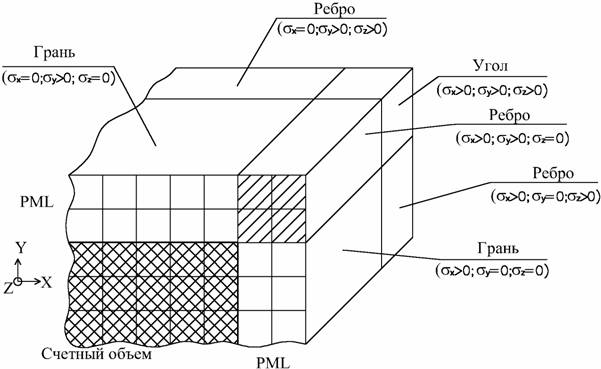
Рис. 1. Счетный объем в окружении слоев PML.
Напоследок примеры программного кода Delphi.
Функция определения геометрического профиля потерь. D – расстояние от интерфейса, dStep – шаг по пространству в том направлении, для которого вычисляется профиль, pmlG - параметр g (коэффициент прогрессии), plmLayerNumber - количество слоев.
function GetSigma(D, dStep: single) : single;
begin
// по Беренгеру - 95
Result:= -(Eps0*C)/(2*dStep) * ln(pmlG)/(Power(pmlG, plmLayerNumber)-1) *
ln(pmlR) * Power(pmlG, D/ dStep);
//функция Power – возведение в степень - в модуле Math;
end;
Ниже код pmlUpdateHXN - процедуры вычисления поля Н для грани Х=Хmax. Массив pmlXN – массив структур, содержащих все 12 векторов ячейки PML. pmlSigmaStarX и pmlExpSigmaStarX – массивы с предварительно вычисленными коэффициентами с учетом профиля потерь. pmlBHY pmlBHZ – коэффициенты с нулевыми потерями. Ребра и углы в этой процедуре не вычисляются. Их вычисление осуществляется в отдельных процедурах, что позволяет ускорить счет и эффективно ввести условия симметрии и PEC для границ PML. Жирным шрифтом выделен фрагмент, вычисляющий поле Н на внешней границе PML: для нулевых векторов Е внешней границы (PEC) не выделяется вообще никакой памяти.
procedure pmlUpdateHXN;
var I,J,K: Integer;
begin
//Hyx
For I:=0 to plmLayerNumberMinus2 do
for J:=0 to YSizeMinus1 do
for K:=0 to ZSizeMinus1 do
begin
pmlXN[I,J,K].Hyx:= pmlSigmaStarX[I]*pmlXN[I,J,K].Hyx+
pmlExpSigmaStarX[I]*(pmlXN[I+1,J,K].Ezx+pmlXN[I+1,J,K].Ezy-pmlXN[I,J,K].Ezx-pmlXN[I,J,K].Ezy);
end;
I:=plmLayerNumberMinus1;
for J:=0 to YSizeMinus1 do
for K:=0 to ZSizeMinus1 do
begin
pmlXN[I,J,K].Hyx:= pmlSigmaStarX[I]*pmlXN[I,J,K].Hyx+
pmlExpSigmaStarX[I]*(0-pmlXN[I,J,K].Ezx-pmlXN[I,J,K].Ezy);
end;
//Hyz
For I:=0 to plmLayerNumberMinus1 do
for J:=0 to YSizeMinus1 do
for K:=0 to ZSizeMinus2 do
begin
pmlXN[I,J,K].Hyz:= pmlXN[I,J,K].Hyz-
pmlBHZ*(pmlXN[I,J,K+1].Exy+pmlXN[I,J,K+1].Exz
- pmlXN[I,J,K].Exy-pmlXN[I,J,K].Exz);
end;
//Hzx
For I:=0 to plmLayerNumberMinus2 do
for J:=0 to YSizeMinus1 do
for K:=0 to ZSizeMinus1 do
begin
pmlXN[I,J,K].Hzx:= pmlSigmaStarX[I]*pmlXN[I,J,K].Hzx-
pmlExpSigmaStarX[I]*(pmlXN[I+1,J,K].Eyx+pmlXN[I+1,J,K].Eyz-pmlXN[I,J,K].Eyx-pmlXN[I,J,K].Eyz);
end;
I:=plmLayerNumberMinus1;
for J:=0 to YSizeMinus1 do
for K:=0 to ZSizeMinus1 do
begin
pmlXN[I,J,K].Hzx:= pmlSigmaStarX[I]*pmlXN[I,J,K].Hzx-
pmlExpSigmaStarX[I]*(0-pmlXN[I,J,K].Eyx-pmlXN[I,J,K].Eyz);
end;
//Hzy
For I:=0 to plmLayerNumberMinus1 do
for J:=0 to YSizeMinus2 do
for K:=0 to ZSizeMinus1 do
begin
pmlXN[I,J,K].Hzy:= pmlXN[I,J,K].Hzy+
pmlBHY*(pmlXN[I,J+1,K].Exy+pmlXN[I,J+1,K].Exz-pmlXN[I,J,K].Exy-pmlXN[I,J,K].Exz);
end;
//Hxy
For I:=0 to plmLayerNumberMinus1 do
for J:=0 to YSizeMinus2 do
for K:=0 to ZSizeMinus1 do
begin
pmlXN[I,J,K].Hxy:= pmlXN[I,J,K].Hxy-
pmlBHY*(pmlXN[I,J+1,K].Ezx+pmlXN[I,J+1,K].Ezy-pmlXN[I,J,K].Ezx-pmlXN[I,J,K].Ezy);
end;
//Hxz
For I:=0 to plmLayerNumberMinus1 do
for J:=0 to YSizeMinus1 do
for K:=0 to ZSizeMinus2 do
begin
pmlXN[I,J,K].Hxz:= pmlXN[I,J,K].Hxz+
pmlBHZ*(pmlXN[I,J,K+1].Eyx+pmlXN[I,J,K+1].Eyz-pmlXN[I,J,K].Eyx-pmlXN[I,J,K].Eyz);
end;
end; //procedure pmlUpdateHXN;
При программировании приходится сталкиваться с некоторыми трудностями. PML -границы окружают счетный объем, поэтому для каждой стороны счетного объема требуется свой массив ячеек PML. Все массивы взаимодействуют не только со счетным объемом (интерфейс "счетный объем" - PML), но и между собой в местах соприкосновения, что создает дополнительные проблемы.
Далее тест на тему сравнения граничных условий. Тест нестандартный, убедительно демонстрирующий превосходство условий PML и влияние частоты fc на результат. По сути, тест двумерный, но проделан в 3D объеме с периодическими границами (с условиями симметрии). Можно назвать такую задачу 2,5-мерной.
файл:/zfdtd/method/abc2.htm