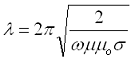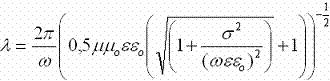На этой страничке находятся дополнительные сведения по методу расчета, которые не вошли в другие разделы сайта и вряд ли вообще встречаются в литературе по FDTD

1. Как вычислить проникновение поля в хороший проводник (например, алюминий), чтобы наблюдать скин-эффект и определить скин-слой? Эта задача решаема, но следует знать, что длина волны в проводнике в тысячи и даже сотни тысяч раз меньше, чем в воздухе. А условие, что шаг по пространству д.б. минимум в 10 раз меньше длины волны никто не отменял.

Длину волны в проводнике можно найти по формуле [1]:

Для медного проводника с проводимостью 6*10⁶ Cм/м на частоте 100 МГц длина волны составляет 0,04 мм или в 73000 раз меньше, чем в воздухе.

Кстати, в материале с проводимостью всего 1 См/м на частоте 1 ГГц длина волны равна 10 см (вместо 30 см в свободном пространстве). Если при этом задать еще и диэлектрическую проницаемость, равную 4, то длина волны станет около 9 см, а не уменьшится еще в 1,41 раза, как может показаться. Найти длину волны в любом материале можно по формуле [1]:

Литература

1. Шимони К. Теоретическая электротехника. М., «Мир», 1964.

2. Как же тогда вообще решаются задачи с проводниками? В большинстве задач поле внутри проводников никого не интересует. А на поверхности граничные условия получаются автоматически и хорошо работают. Т.е. поля вокруг проводника и на его поверхности правильные, а внутри – с ошибкой, причем в тысячи раз. Ошибка в том, что поле внутри проводника, хотя и ослабляется, но все же получается гораздо больше, чем должно быть. Так что правильно вычислить ослабление поля сплошным медным экраном толщиной 4 мм на частоте 100 МГц при шаге по пространству 1 мм не удастся, т.к. проникающее поле будет больше реального в тысячи раз, хотя меньше падающего тоже в тысячи раз. Все будет правильно внутри экрана, если вы выполните условие 1/10 длины волны из ответа на предыдущий вопрос. А на поля снаружи и токи по поверхности эта ошибка, как показывает практика, не влияет.

3. При решении задачи проникновения поля в материал с потерями (проводимость равна 1 См/м, частота 1 ГГц) вместо синусоиды на глубине метра получился длинный, похожий на двухэкспоненциальный, импульс. Почему?

Причина кроется в низших гармониках и частотной дисперсии. Когда синусоида только начинается, первый полупериод содержит все нижние гармоники от нулевой частоты. Низкие частоты в материале с потерями затухают во много раз медленнее, чем высокие. Поэтому, хотя низких частот в спектре мало, они преобладают на больших глубинах в материале, там, где основная частота уже сильно, на несколько порядков, уменьшилась.

Выход из данной ситуации – это задать синусоиду с очень медленно нарастающей амплитудой, что позволит снизить уровень паразитных нижних гармоник.

4. При расчете проникновения поля через щель в сплошном экране результат получился неправильным, рассчитанное поле внутри оказалось гораздо больше по амплитуде и каким-то изрезанным. Почему?

Такой результат может быть получен как отклик на импульсное или синусоидальное воздействие. Причина проста: в спектре исходного сигнала были высшие гармоники, которые имеют длину волны меньше, чем 10 шагов по пространству. Пусть этих гармоник было всего 1 %, но в щель они проникают в 100 раз интенсивнее. Длина этих волн слишком маленькая для выбранного шага по пространству, они вычисляются с очень большой ошибкой и искажают результирующее поле за щелью. Даже синусоидальный сигнал, если он начинается сразу с максимальной амплитуды, имеет много высших гармоник. Для устранения ошибки необходимо брать сигнал с гораздо меньшим уровнем недопустимых гармоник. Синусоида должна плавно увеличивать свою амплитуду, а для широкополосных входных сигналов можно взять «хитрый» сигнал Sin(X)/X, спектр которого постоянный от нуля до заданной частоты, а затем резко уменьшается практически до нуля. Другие сигналы, нужно брать осторожно, обязательно проверять их спектр. Особенно осторожно надо быть с двухэкспоненциальным импульсом, который имеет разрыв первой производной в начале импульса и этим производит много высших нефизичных гармоник.

5. Как правильно задавать щель в экране?

Допускается задавать щель всего в одну ячейку шириной.

Не нужно забывать при моделировании, что толщина экрана оказывает заметное влияние на проникновение поля: чем толще экран, тем хуже поле проникает через щель.

6. При решении задачи, в которой счетный объем заканчивается границей PML, задавалось внешнее поле, а от границы до объекта 9 ячеек, через 60 тысяч шагов пропала устойчивость. Как исправить ситуацию?

Да, границы PML при задании внешнего поля могут терять устойчивость при большом количестве шагов по времени. Причина в том, что при задании внешнего поля поле на границах счетного объема задается аналитически, а внутри вычисляется по конечно-разностному алгоритму. Ошибка конечно-разностной аппроксимации внутри объема накапливается и, в конце концов, поле на границах, задаваемое аналитически, не совпадает с полем внутри. Это приводит к потере устойчивости. Первейшая причина ошибки – недостаточная точность вычислений при использовании арифметики с одинарной точностью. А именно такая точность чаще всего используется в программах, в т.ч. и FDTDpro. Но и двойная точность не исключает потери устойчивости. При использовании арифметики с двойной точностью проблемы возникают позже, при большем количестве шагов счета.

Бороться с потерей стабильности можно. Устойчивость растет в трех случаях:

1. Удаляются границы от объекта;

2. Растет количество слоев PML;

3. Увеличивается задаваемый коэффициент отражения от границ.

Вероятно, при любых ухищрениях стабильность всегда рано или поздно будет теряться, но можно добиться, чтобы она терялась после того, как задача уже решена.

Потеря устойчивости проявляется в появлении высокочастотных, экспоненциально нарастающих колебаний, так что распознать ее несложно.

Имеется продолжение (см. содержанние)