Сайт Александра Зеленина
Вычисление электромагнитного поля в дальней зоне с использованием метода FDTD и интеграла Кирхгофа.
Александр Зеленин
2006 г
В сокращенном и измененном виде материал опубликован в журнале «Технология ЭМС» 2 кв. 2006, а также на конференции по ЭМС-2006 (СПб)
Решение уравнений Максвелла методом FDTD дает возможность вычисления электромагнитного внутри некоторой ограниченной области пространства. Ограничение на размеры области, в которой проводятся вычисления, определяются ограниченной вычислительной мощностью применяемых ЭВМ, а именно тремя факторами: ограниченной скоростью выполнения арифметических операций, ограниченным объемом оперативной памяти и ограниченной скоростью обмена данными между процессором с памятью. Однако существует ряд задач, в которых необходим расчет электромагнитных полей на больших расстояниях от некоторого объекта, излучающего или рассевающего электромагнитное поле. В их числе расчет диаграммы направленности антенн, определение эффективной поверхности отражения радиолокационных целей, решение задач дифракции и. др. В данной статье предложен эффективный способ вычисления полей в дальней зоне с использованием результатов вычислений ближнего поля методом FDTD. Под дальним полем здесь подразумевается поле за пределами вычислительного объема, а ближнее поле здесь означает поле, вычисляемое непосредственно методом FDTD.
Преобразование ближнего поля в дальнее поле с использованием интеграла Кирхгофа
Существует несколько методов преобразования ближнего поля в дальнее поле. Все они включают интегрирование по замкнутой поверхности, которая охватывает излучающий или рассеивающий объект. А в остальном имеются значительные отличия. Одни методы интегрируют, используя поверхностные эквивалентные токи (электрические и магнитные), другие непосредственно используют поля Е и Н. Одни методы применяются в частотной области, другие работают во временной области.
Например, для вычисления дальнего поля часто применяют интегрирование по элементам, на которые разбивается замкнутая поверхность. Каждый элемент поверхности является элементарным электрическим и магнитным диполем одновременно. Если при этом ближнее поле вычисляется методом FDTD, выполняются следующие операции:
- Все компоненты E и H полей на поверхности, по которой происходит интегрирование, сохраняются на всех шагах по времени. Т.е. к концу вычислений известна временная форма поля в каждой точке поверхности.
- Поля Е и Н на поверхности преобразуются в эквивалентные электрические и магнитные токи.
- Осуществляется преобразование токов на поверхности в частотную область.
- Вычисляются составляющие Eφ, Eθ, Еr и соответствующие составляющие поля H для всех частот и от каждого элемента Гюйгенса на поверхности. Элементы Гюйгенса в данном случае - это обычные ячейки FDTD. С каждой ячейкой сопоставляется своя собственная система полярных координат.
- Значения Eφ, Eθ, Еr и соответствующих составляющих поля H преобразуются в прямоугольные координаты (Ex, Ey, Еz) и складываются в точке наблюдения. Только на этом шаге происходит собственно интегрирование по поверхности.
- Производится обратное преобразование во временную область. Теперь искомое поле найдено.
Существует ряд модификаций приведенного метода расчета дальнего поля, но при применении метода FDTD более логичным выглядит вычисление поля в дальней зоне с использованием только временной области и без преобразования полей в эквивалентные токи. Кроме того, желательно обойтись без преобразования в другие системы координат. Такой метод существует – это вычисления с использованием поверхностного интеграла Кирхгофа.
Способ применения поверхностного интеграла Кирхгофа совместно с методом FDTD приводится в [3]. Однако в [3] допущены три грубые ошибки в формулах. Кроме того, в порядок самого интегрирования введена путаница. Пришлось заново вывести формулы, воспользовавшись идеей Рамахи (Ramahi, автор [3]). Результат получился хорошим, поэтому, несмотря на досадные ошибки в статье, хочется выразить автору свою благодарность.
Интеграл Кирхгофа связывает поле внутри ограниченного объема с полем и его производными на поверхности, ограничивающей объем. Эта формула выведена в середине 19 века немецким физиком Г. Кирхгофом, и во временной области имеет вид [3]:
|
|
(6) |
где p, p’ – точка наблюдения
и точка на поверхности соответственно; ñ – единичный вектор
нормали к поверхности; Ψ – скалярная функция, которая может быть
любой из шести компонент поля; R – расстояние от точки наблюдения до точки на поверхности; ![]() - вектор p ‑ p’; с – скорость света; A’
– площадь элемента поверхности. В формуле (6) ret
означает, что интегрирование осуществляется с учетом запаздывающего времени t’ = t ‑ R/c. Вектор нормали направлен внутрь замкнутого объема.
- вектор p ‑ p’; с – скорость света; A’
– площадь элемента поверхности. В формуле (6) ret
означает, что интегрирование осуществляется с учетом запаздывающего времени t’ = t ‑ R/c. Вектор нормали направлен внутрь замкнутого объема.
Формула (6) выражает принцип Гюйгенса, согласно которому каждая точка на волновом фронте служит фиктивным источником воображаемой сферической волны. Каждый участок поверхности dA’ излучает волну, которая в точку наблюдения p приходит с задержкой R/c. При этом на каждом шаге FDTD по времени на поверхности интегрирования возникает совокупность фиктивных источников, поле от которых придет в точку наблюдения с разным запаздыванием, поскольку расстояние R для всех точек различно. Это означает, что на одном временном шаге FDTD из (6) получаются вклады участков dA’ в разные временные участки выходного сигнала в точке наблюдения.
Шаг по времени при вычислении интеграла (6) тесно связан с шагом по времени FDTD и равен ему. Выходная последовательность в точке наблюдения имеет такой же шаг по времени. Однако задержка R/c может не быть кратной шагу по времени. Поэтому получаемое время задержки округляется до ближайшего времени, кратного шагу FDTD. Возникающая при этом ошибка незначительна, т.к. шаг по времени в классическом FDTD мал по сравнению с периодом колебаний вычисляемого сигнала.
Чтобы привести (6) к виду, удобному для применения совместно с алгоритмом FDTD, необходимо выполнить ряд преобразований. При этом учтем, что все участки поверхности, по которой ведется интегрирование, в алгоритме FDTD всегда перпендикулярны одной из осей координат.
Предположим, что поверхность dA’ перпендикулярна оси Z и точка p’ имеет координаты (i, j, ko) (рис. 2).
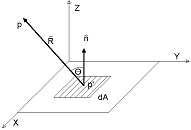
(рис. 2).
Применим преобразование подынтегральных слагаемых (6) в конечные разности:
|
|
(7) |
Для упрощения дальнейшей записи введем обозначения:
|
|
(8) |
и применим стандартные для FDTD обозначения для дискретных значений времени: Ψ(t’) = Ψ(n+1), Ψ(t’-Δt) = Ψ(n), Ψ(t’+ Δt) = Ψ(n+2). Кроме того, вспомним, что время в точке наблюдения t = t’ + R/c . Округляя t до ближайшего целого шага по времени обозначим его как tn*.
Выражение (6) с учетом введенных обозначений (7) и (8) запишется для одной площадки dA в виде:
|
|
(9) |
где Ai,j = Δx Δy.
В (9) нет смысла записывать сумму по всем участкам поверхности, т.к. tn* в общем случае для каждого участка имеет разное значение, поскольку различно расстояние R. Временная последовательность в точке наблюдения p получается суммированием значений Ψ(p, tn*) на каждом шаге по времени по всем участкам поверхности с учетом времени запаздывания.
В (9) значение функции Ψ(p, tn*) вычисляется с использованием значений Ψ на трех шагах по времени. Но это не означает, что необходимо всегда помнить значения двух предыдущих шагов. Сгруппируем слагаемые (9) по временным шагам и запишем в виде:
|
|
(10) |
где
|
|
(11) |
В приведенных (10) и (11) присутствуют шаги n, n+1 и n+2. Но можно вычислить все эти значения для одного шага, допустим, текущего шага n+1. Тогда, если считать, что вычисляется шаг n+1, то F1(n) добавляется в tn+1*- шаг вычисляемой последовательности. F2(n+1) добавляется в предыдущую временную точку tn*, а F3(n+2) добавляется еще на один временной шаг раньше в вычисляемой последовательности (tn-1*). В этом случае F3(n+2) = ‑ F1(n).
Так что не требуется хранить значения полей на поверхности интегрирования. Но для ускорения вычислений можно заранее вычислить значения расстояний и косинусы углов от всех участков поверхности до точки наблюдения.
Вместо функции Ψ можно свободно подставлять Ex, Ey, Ez, Hx, Hy или Hz.
Все компоненты ячейки Yee находятся в разных местах пространства. Но расстояния и косинусы углов вполне можно вычислить общие для всех компонент. Главное, чтобы они принадлежали одной ячейке. Тогда при вычислении дальнего поля рассчитанные компоненты также окажутся сдвинутыми в пространстве, что удобно использовать при тестировании программы, когда поле одновременно, в одной и той же ячейке, вычисляется как непосредственно алгоритмом FDTD, так и решением поверхностного интеграла Кирхгофа.
Здесь приведен вывод формулы только для одной поверхности. Для остальных пяти поверхностей вывод формул аналогичен. Интегрирование следует вести строго по замкнутой поверхности.
Границы интегрирования можно приблизить вплотную к объекту, заданному в расчетах FDTD.
При вычислении полей на довольно больших расстояниях из уравнения (9) можно исключить слагаемое, убывающие как 1/R2, а угол направления на точку наблюдения вычислить один на всю грань поверхности интегрирования. Этот случай соответствует случаю дальней зоны в ее обычном понимании и позволяет ускорить расчеты и уменьшить требуемую для расчетов память.
Численные результаты.
Для тестирования приведенного в настоящей статье способа вычисления интеграла Кирхгофа проведен тест, в котором вычисление поля в дальней зоне проводится для точки, которая находится внутри вычислительного объема. Это позволило сравнить полученные результаты с расчетом непосредственно методом FDTD.
Геометрия задачи показана на рис. 3. Задача решалась в сетке 150х50х50 ячеек, шаг по пространству 1 см по всем направлениям. Объект – хорошо проводящее кольцо диаметром 33 см и высотой 33 см. Толщина стенок кольца 1 см. Ось кольца параллельна оси Y. Центр кольца имеет координаты (25, 25, 25). На кольцо падает плоская волна по направлению оси X. Вектор E параллелен оси Z. Форма поля – радиоимпульс с несущей частотой 1500 МГц и амплитудой 1 В/м. Граничные условия – восемь слоев PML c коэффициентом отражения 0,001 %. Граница интегрирования находится в трех ячейках от объекта.

Рис. 3.
В точке наблюдения с координатами (140, 25, 25) осуществлялся вывод всех составляющих вектора E для рассеянного поля как непосредственно из расчетов FDTD, так и путем решения интеграла Кирхгофа. Результаты сравнивались между собой. На рис. 4 изображена картина поля, полученная в процессе вычислений.
![]()
Рис. 4
Получены следующие результаты. Компонента Ez, самая большая по амплитуде (600 мВ/м), имеет отличие 1,7 %, компонента Ex (3,2 мВ/м) отличается на 0,6 %. Компонента Ey должна быть равна нулю, но при нахождении интеграла Кирхгофа получен импульс амплитудой 15 мкВ/м, что в 40 тыс. раз меньше, чем амплитуда компоненты Ez.
На практике погрешность определения слабовыраженных составляющих не играет роли. Погрешность вычисления главных составляющих поля, как показал ряд тестовых расчетов для различных геометрий, не превышает 5 % и обычно лежит в диапазоне (1-3) % для случая вычисления ближнего поля. При вычислении поля на значительном удалении погрешность уменьшается. Проиллюстрируем это примером.
Другой пример – решение задачи определения эффективной площади отражения (ЭПО) для случая отражающей пластины квадратного сечения. В этом случае известно аналитическое выражение для ЭПО. Возьмем квадратную идеально проводящую пластину. В случае, если длина волны много меньше стороны квадрата, ЭПО вычисляется по формуле:
|
|
(12) |
где σ – ЭПО, a – сторона квадрата, λ – длина волны.
В то же время, через напряженность поля ЭПО выражается как:
|
|
(13) |
где R – расстояние от объекта до точки наблюдения, Es – напряженность рассеянного поля на расстоянии R, Ei – напряженность поля, падающего на объект. Формула (12) справедлива для случая, когда поле падает перпендикулярно поверхности пластины, а (13) - когда точка наблюдения находится в направлении, обратном направлению распространения падающей волны.
Подставляя (12) в (13) и выражая Es, получим:
|
|
(14) |
Для квадратной пластины размерами со стороной а=1 м, при длине волны λ=0,1 м с Ei=1 В/м на расстоянии R=1000 м по (14) получаем Es = 0,01 В/м.
Эта же задача была решена методом FDTD с применением интеграла Кирхгофа для двух случаев. В первом случае шаг по пространству равен λ/10, 150 шагов счета; в другом – λ/20, 300 шагов счета (1 см и 5 мм соответственно). В первом случае получено Es=0,0097 В/м, во втором - Es=0,0101 В/м. Погрешность 3 % и 1 % находится в пределах погрешности метода FDTD для соответствующего соотношения длины волны и шага по пространству.
Задача решалась в объеме 20х120х120 ячеек, шаг 1 см и с удвоенным значением объема с шагом 5 мм. Границы – 8 слоев PML. Границы интегрирования располагались в 3-х ячейках от пластины.
На рис. 5. приведена напряженность поля на расстоянии 1000 м от пластины в зависимости от направления, вычисленная с шагом 5 o. Ноль градусов совпадает с направлением распространения падающей волны.
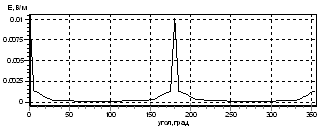
Рис. 5.
Выводы
Применение поверхностного интеграла Кирхгофа совместно с методом FDTD расширяет область применения метода. Такой гибрид эффективен при расчетах диаграмм направленности антенн, эффективной площади отражения и в других случаях, где требуется найти поле на некотором удалении от объекта.
Точность вычислений с использованием поверхностного интеграла Кирхгофа соизмерима с точностью самого метода FDTD.
Литература
1. K. S. Yee, “Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media,” IEEE Transactions on Antennas and Propagation, vol. 14, pp. 302-307, May 1966.
2. А.Тафлав, К. Р. Умашанкар. Численное моделирование рассеяния электромагнитных волн и вычисление эффективной площади отражения целей конечно-разностным методом во временной области. ТИИЭР, т. 77. № 5, май 1989.
3. O. M. Ramahi, “Near- and far-field calculations in FDTD simulations using. Kirchhoff surface integral representation”, IEEE Transactions on Antennas and Propagation, vol. 45, no 5, may 1997.
файл:/zfdtd/method/n2f.htm

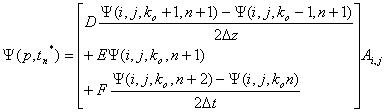 ,
,