Сайт Александра Зеленина

Задание произвольного направления движения плоской волны электромагнитного поля

Александр Зеленин

2006 г

Здесь показан вывод уравнений, позволяющих легко задавать любое направление прихода электромагнитной волны для случая плоской волны.

Предположим, что нам необходимо задать произвольное направление падения плоской электромагнитной волны. Это означает, что необходимо задать плоскость, параллельную фронту будущей волны. Плоскость удобно задавать с помощью вектора нормали, а вектор нормали, вращающийся на все 360 ^o, удобно задать в полярных координатах. Поэтому на время отвлечемся от прямоугольных координат и перейдем к полярным (рис. 1), а уже них к прямоугольным, также показанным на рисунке.

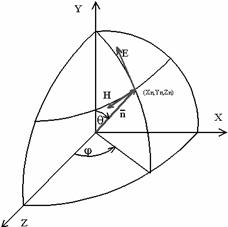
Рис. 1.

Направление вектора нормали n задается всего двумя углами θ и φ. Угол θ определен в диапазоне {0…180^o}. Угол φ определен в диапазоне {-180^o…180^o}. Длина вектора равна единице, вектор начинается в начале координат и заканчивается в точке (Xn, Yn, Zn). В нашей задаче вектор n совпадает с направлением движения плоской электромагнитной волны.

Координаты конца вектора n в прямоугольных координатах равны направляющим косинусам вектора и находятся как:

Xn = sin(φ)√(1- cos(θ)²)

Yn = cos(θ)

Zn = cos(φ)√(1- cos(θ)²)

На рис. 1 рассматривается случай, когда вектор Е лежит в вертикальной плоскости. Для этого случая все компоненты поля в прямоугольных координатах выражаются как:

Ex = -E cos(θ) sin(φ)

Ey = E sin(θ)

Ez = -E cos(θ) cos(φ)

Hx = H sin(φ)

Hy = 0

Hx = -H cos(φ)

Итак, по двум углам θ и φ однозначно определяются все компоненты поля. Осталось определить расстояние R от плоскости до произвольной точки пространства, в которой определяется падающее поле. Расстояние R определяет задержку поля от плоскости до данной точки пространства.

Если плоскость проходит через начало координат, то нетрудно показать, что кратчайшее расстояние от плоскости до любой точки пространства (Xo, Yo, Zo) определяется как:

R = Xo Xn + Yo Yn + Zo Zn,                                                     (1)

причем в направлении вектора n расстояние R имеет положительное значение, в обратном направлении – отрицательное. Это свойство легко использовать для определения расстояния в случае, если плоскость должна проходить не через начало координат (напомним, что в рассмотренном случае вектор n начинается из начала координат и, следовательно, плоскость также проходит через начало координат), а через любую вершину или грань области полного поля, показанную на рис. 1. И при этом вся область полного поля оказывается в полуплоскости по положительному направлению n. Для этого нужно вычислить наименьшее расстояние от плоскости, проходящей через начало координат, до всех вершин области полного поля по (1). Обозначим найденное наименьшее расстояние через Rmin.

Расстояние от той границы (или вершины) области полного поля, где задержка поля равна минимальному значению (нулю) (обозначим его R’), до любой точки вычислительного объема находится как:

R’= R - Rmin

Следует добавить, что Rmin вычисляется не по модулю расстояний, а с учетом знака. Знак R также ни в коем случае не отбрасывается. В итоге величина R’ всегда положительная в пределах области полного поля.

По известному расстоянию R’ обычным путем находится время задержки движения поля от плоскости до заданной точки границы полного поля.

Если направление движения волны задавать в сферических координатах, то углы легко преобразуются к углам полярных координат, а далее процедура вычислений такая же, как описано в текущем разделе. В прямоугольных же координатах задавать направление неудобно.