Сайт Александра Зеленина

Навигация по подразделам главы:

[9.1] - [9.2] - [9.3] - [9.4] - [9.5] - [9.6] - [9.7]

9.7. Определение КПД сжатия по опытам Пархомова

Казалось бы, что накоплено довольно много публикаций, связанных с опытами с никель-водородными реакторами. Но при внимательном рассмотрении этих публикаций выясняется, что в целях каких-либо численных оценок опереться почти не на что.

Наиболее известными являются опыты А. Росси, вернее, демонстрация им работающих реакторов. Все они оказались обычными фокусами. Примитивность фокусов с технической стороны не сразу была осознана LENR-сообществом, потому что Росси привлек к фокусам нескольких ученых из разных стран (Италия и Щвеция). Авторитет этих ученых долго не давал в сообществе сказать фразу «А король-то голый». Сам Росси является, можно сказать, предводителем шайки мошенников из привлеченных им «независимых профессоров» и «экспертов». Цель этой шайки – обмануть потенциальных инвесторов и заставить их раскошелиться – была успешно реализована в известной истории с компанией Industrial Heat. Росси по-прежнему (на начало 2019 года) ищет очередную жертву, раскинув паутину лжи.

Реакторы А. Г. Пархомова построены на базе продемонстрированного Росси в 2014 году фокуса «Лугано». Но у Пархомова реакторы в ряде опытов демонстрировали избыточное тепло.

В самом начале своего пути Пархомов А.Г. путем титанических усилий провел множество опытов и сумел получить несколько удачных результатов. В [17] он приводит результаты испытаний шестнадцати (!) реакторов. Из них восемь «боевых» с топливом, и восемь «холостых» без топлива. Четыре «боевые» реактора продемонстрировали наличие заметного избыточного тепла. Были ли эти реакторы идентичны друг другу? Возможно. Если реакторы были идентичны, то все они содержали 1 грамм порошка никеля и их можно сравнивать по удельной мощности. Удельная мощность, полученная по данным из [17], приведена в таблице 9.2.

Таблица 9.2. Удельная мощность в четырех экспериментах Пархомова А. Г.

Температура измерялась не в порошке никеля, а снаружи керамической трубки. С учетом сравнительно невысокой теплопроводности керамики на стенке трубки (толщиной 2,5 мм) должен возникнуть перепад температур тем больший, чем больше избыточная мощность. Поэтому первые два результата из табл. 9.2, несмотря на одинаковую температуру снаружи, имеют разную температуру внутри. При мощности 123 Вт температура порошка никеля была больше, чем при мощности 57 Вт. Почему так? Давайте посчитаем.

Внутренний диаметр трубки был 5 мм. Эта трубка заполнена смесью порошка никеля (1 грамм) и алюмогидрида лития (0,1 грамм). Длину засыпки и марку порошка никеля Пархомов не сообщает. Но, если считать, что насыпная плотность никеля равна 2 г/см³, а у алюмогидрида 0,2 г/см³, то длина засыпки будет около 5 см.

Пренебрегая для простоты потоком тепла через торцы для цилиндрической геометрии получим, что вся избыточная мощность выходит через стенку толщиной 2,5 мм. Считая теплопроводность керамической стенки 4 Вт/м/К получим разность температур:

R1=2.5e-3 //внутренний радиус трубки, м

R2=5e-3 //наружный радиус трубки, м

P=123 // тепловая мощность, Вт

Lambda= 4 // теплопроводность, Вт/м/К

L= 5e-2 //длина засыпки

Tнар-Твн = P*ln(R2/R1)/2/pi/L/Lambda = 68 градусов.

Для всех четырех случаев температура внутри приведена в табл. 9.3.

Таблица 9.3. Температура внутри в четырех экспериментах Пархомова А. Г.

В том случае, если длина засыпки отличается от 5 см, то перепад температуры на стенке обратно пропорционален длине засыпки.

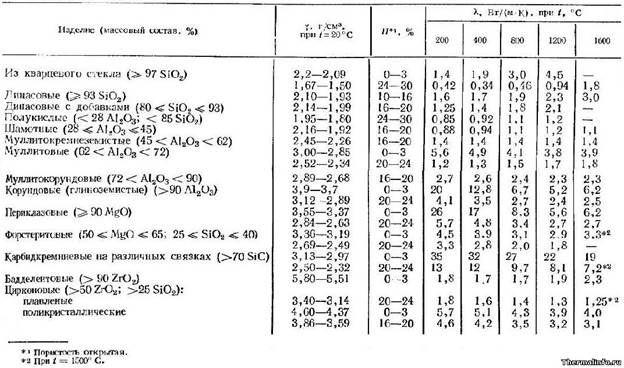
Нужно признать, что теплопроводность 4 Вт/м/К, принятая в расчетах, может отличаться от настоящей, и скорей всего эта цифра завышена. Возможные варианты теплопроводности представлены в табл. 9.4. Конкретный сорт керамики, которую применил Пархомов, никому неизвестен.

Таблица 9.4. Теплопроводность керамики.

Что можно сказать по данным в таблице 9.3? Результат в последнем столбце (1768 С), там, где избыточная мощность 866 Вт, дает температуру внутри на три сотни градусов выше точки плавления никеля (1453 С). Но никель не стекал на дно канала, а оставался в пористой массе «топлива» в виде мелких капель. Поэтому есть вероятность, что при жидком состоянии никеля в нем также распространяются водородные волны, как и в твердом состоянии.

Рост удельной мощности при возрастании температуры связан с ростом КПД водородных волн. После расплавления никеля вероятнее всего КПД увеличивается скачком и далее остается постоянным. Проверить это предположение в настоящее время не представляется возможным.

Чтобы по данным Пархомова оценить КПД, нужно определить частоту колебаний. Нам известно, что в реакторах Пархомова был водород. В таблице 9.3 есть расчетная температура. Есть данные о длине керамических трубок – 120 мм. На этой длине возможен акустический резонанс с длиной волны 240 мм. По скорости звука можно определить резонансную частоту. Неизвестным является давление, поэтому примем его равным атмосферному. В Справочнике [28] найдем скорость звука: 2785 м/с при температуре 1400 К (1127 C) и 2886 м/с при температуре 1500 К (1227 C). Для более высоких температур данные о скорости отсутствуют. Так как при росте температуры на 100 К скорость звука растет приблизительно на 100 м/с, то можно оценить скорость звука и резонансную частоту при нужных нам температурах, а также получить величину КПД, применяя формулы из п. 9.5. Результаты расчета приведены приведены в таблице 9.5.

Таблица 9.5 – Скорость звука в водороде, частота резонанса в опытах Пархомова и КПД сжатия водородной волны

Наблюдаемый в опытах Пархомова рост мощности от температуры может происходить не только от роста частоты колебаний водорода и роста КПД, но и от роста давления акустической волны. В этом случае КПД будет расти медленнее, чем получено в таблице 9.5.

В заключение текущей главы рассмотрим допустимые размеры частиц никеля, опираясь на полученные данные о КПД. Результаты расчетов минимального радиуса шариков никеля приведены в табл. 9.6.

Таблица 9.6 – Минимально допустимый размер частиц никеля при амплитуде колебаний давления 5 кПа

Полученные минимальные радиусы вычислены для случая, когда всего два атома водорода подвергаются необходимому сжатию. С ростом амплитуды колебаний давления эти радиусы уменьшаются.

Низкий КПД в опытах Пархомова при 1100-1150 градусах не означает, что при этих температурах он действительно такой. На результат вычисленных КПД могут влиять следующие взаимосвязанные факторы:

- множество частиц порошка никеля имеют радиус ниже барьера (т.е. минимального радиуса) и не участвуют в реакции;

- амплитуда колебаний звуковой волны недостаточна для малых частиц.

В этих случаях не весь никель участвует в реакции, а только частицы, начиная с определенного размера и поэтому получается низкий КПД.

Но, если спускаться вниз по температуре, то тенденция снижения КПД наблюдается в опытах Пиантелли. В одном из опытов Пиантелли стержень массой 16 грамм производил около 50 Вт мощности. Это составляет всего 3 Вт/г. Длина ячейки была 100 мм, температура около 500 С. Скорость звука в водороде 2 км/с, частота колебаний 10 кГц. Вычисленный КПД составил около 0,01 при амплитуде колебаний давления 5 кПа.

Но у Пиантелли, как он утверждал и что вполне вероятно, в реакции участвовал только поверхностный слой никелевого стержня. Если принять толщину слоя 200 мкм, то удельная мощность получится в 6,5 раз больше, т.е. около 20 Вт/г. КПД тоже получится выше: 0,025. А если  принять толщину слоя 100 мкм, то КПД приблизится к результату Пархомова при температуре 1150 С.

Во всех расчетах, приведенных в этом подразделе, добротность колебательной подсистемы водорода в никеле была принята равной 1, а потери мощности на возбуждение акустических колебаний в газовой фазе водорода не учитывались. Сближение водорода (величина N из (9.4)) принято равным 50.

Происхождение акустических волн в никель-водородных реакторах будет рассмотрено в следующей главе.

>>>Далее>>>

Навигация по подразделам главы:

[9.1] - [9.2] - [9.3] - [9.4] - [9.5] - [9.6] - [9.7]